Ich übersetze hier verschiedene Beispiele, die für den Schulunterricht gedacht sind, in Euler. Bisweilen erlaube ich mir zusätzliche Anmerkungen zu der Vorgehensweise. Es geht aber hauptsächlich darum zu zeigen, wie Euler für solche Aufgaben eingesetzt werden kann.
In einer Abiturarufgabe aus dem alten G9 mit Leistungskursen ist die folgende Funktion gegeben. Die Aufgabe ist nach meiner Meinung nicht geeignet, Mathematik in moderner Art zu lehren. Ich habe die Aufgabe auf der folgenden Webseite gefunden.
Die Aufgabe startet mit der folgenden Funktion.
>function f(x,t) &= -1/9*x^4+2/3*t^2*x^2
2 2 4
2 t x x
------- - --
3 9
Die Aufgaben, die darauf folgen, sind zum Teil sehr leicht zum Einsteigen. Die Frage nach der Symmetrie ist etwa trivial, ebenso wie die Schnittpunkte mit der x-Achse.
Diese Formulierung zeigt übrigens das geometrische Denken, das bei Funktionen eigentlich nicht angebracht ist.
>&solve(f(x,t)=0,x)
[x = - sqrt(6) t, x = sqrt(6) t, x = 0]
Es folgt die Untersuchung auf lokale Extrempunkt und Wendepunkte "des Graphen".
>kp &= solve(diff(f(x,t),x)=0,x)
[x = - sqrt(3) t, x = sqrt(3) t, x = 0]
Vermutlich soll man nun die zweite Ableitung in diesem Punkten berechnen.
>f2 &= diff(f(x,t),x,2); &makelist(f2 with kp[n],n,1,3)
2 2 2
8 t 8 t 4 t
[- ----, - ----, ----]
3 3 3
Man erkennt lokale Minima und Maxima.
Dieses Vorgehen ist nicht sinnvoll. Statt dessen sollte man die Funktion selber in den kritischen Punkten auswerten.
>&makelist(f(x,t) with kp[n],n,1,3)
4 4
[t , t , 0]
Man erkennt sofort die beiden globalen Maxima durch Betrachtung der Grenzwerte
![]()
Außerdem erkennt man, dass 0 nur ein lokales Minimum ist. Die Wendepunkte sind die folgenden.
>&solve(diff(f(x,t),x,2),x)
[x = - t, x = t]
Es wird weiter gefragt, auf welcher Kurve die "lokalen" Maximalpunkte liegen. Dies ist Normalfall eine schwierigere Aufgabe. Uns liegt die Kurve nämlich zunächst nur in Parameterform vor.
![]()
Das lässt sich hier recht einfach als Graph einer Funktion schreiben. Dazu löst man die erste Gleichung nach t auf und setzt in die zweite Gleichung ein.
>&solve(x = (x with kp[1]),t); &y = (f(x,t) with %)
4
x
y = --
9
Nun wird eine Skizze der Funktion für t=2 verlangt. Per Hand muss man also die Nullstellen, die Extremalpunkt und die Wendepunkt eintragen und einen "sinnvollen" Graph dazu zeichnen.
Mit einer Software wie Euler ist das natürlich einfacher.
>plot2d("f(x,2)",-5,5);
Wir tragen noch die bekannten Punkte ein.
>x=[-sqrt(6)*2,sqrt(6)*2,-sqrt(3)*2,sqrt(3)*2,-2,2,0]; y=f(x,2); ... plot2d(x,y,>points,>add):
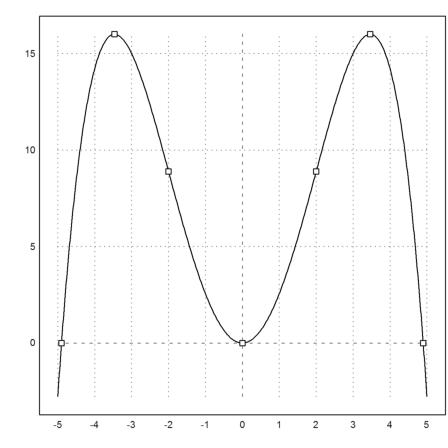
Von nun an werden die Aufgaben etwas schwieriger. Gegeben sind die Punkte
![]()
Ich kann mir eine Seitenbemerkung nicht verkneifen. Diese seltsam altertümliche Notation ist in Schulen übrigens noch üblich. Ob die Schule glaubt, dass sich die Universitäten nach Ihnen richten?
Die Interpolationsaufgabe mit einer Parabel wird wieder geographisch gestellt. Vermutlich sollen die Schüler erkennen, dass die quadratische Funktion die Form
![]()
haben muss. Dann ist das folgende natürlich trivial.
>&solve(a*(t^2 - 6*t^2)=5/9*t^2,a); &y = a*(x^2-6*t^2) with %
2 2
6 t - x
y = ---------
9
Diese Funktion taucht dann nicht mehr auf. Vielleicht hätte man diese Zusatzaufgabe weglassen sollen?
Nun wird ein Dreieck durch
![]()
und "den Schnittpunkt S der Verbindungsgerade duch die beiden Maximumspunkte mit der y-Achse" gebildet, eine Formulierung, die schon beinahe als verwirrend zu bezeichnen ist. Es wird gefragt für welches x_p dieser Flächeninhalt maximal wird.
Die Formel für die Fläche ist mit ein wenig Geometrie leicht zu finden.
>D &= x*(f(2*sqrt(2),2)-f(x,2))
4 2
x 8 x 128
x (-- - ---- + ---)
9 3 9
Die Ableitung ist eine quadratische Gleichung in x^2.
>Ds &= solve(diff(D,x)), Ds()
2 sqrt(sqrt(41) + 9) 2 sqrt(sqrt(41) + 9)
[x = - --------------------, x = --------------------,
sqrt(5) sqrt(5)
2 sqrt(9 - sqrt(41)) 2 sqrt(9 - sqrt(41))
x = - --------------------, x = --------------------]
sqrt(5) sqrt(5)
[-3.51034, 3.51034, -1.44135, 1.44135]
Die Lösung ist offenbar x=1.44..., also
![]()
Die Rechnung per Hand kostet natürlich Zeit und ist fehleranfällig. Übrigens auch die Eingabe der Lösungen per Software.
Eine weitere fehleranfällige Rechnung versteckt sich im letzten Teil dieser Aufgabe. Gefragt wird nach der Fläche F zwischen den folgenden drei Kurven.
>plot2d("f(x,2)",0,2); ...
plot2d(&f(2,2)+diffat(f(x,2),x=2)*(x-2),>add); plot2d("0",>add):
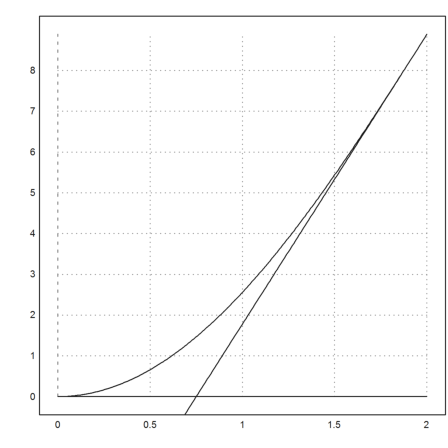
Wir ermitteln zunächst die Tangentengleichung.
>T &= f(t,t) + diffat(f(x,t),x=t)*(x-t)
3 4
8 t (x - t) 5 t
------------ + ----
9 9
Wir benötigen noch die Nullstelle der Tangenten.
>&solve(T=0,x); xzero &= x with %
3 t
---
8
Nun folgt eine per Hand etwas längliche Rechnung, die aber mit Software gut zu machen ist.
>& integrate(f(x,t),x,0,xzero)+integrate(f(x,t)-T,x,xzero,t)
5
19 t
-----
720
Viel besser geeignet um Mathematik zu motivieren, sind Stochastikaufgaben. Die folgende Aufgabenreihe habe ich auf
gefunden.
"Nachdem die Verfilmung eines bekannten Romans erfolgreich in den Kinos gezeigt wurde, veröffentlicht eine Tageszeitung das Ergebnis einer repräsentativen Umfrage unter Jugendlichen. Der Umfrage zufolge hatten 88% der befragten Jugendlichen den Roman zum Zeitpunkt des Kinostarts noch nicht gelesen, 18% sahen die Verfilmung. Von den Befragten, die laut Umfrage den Roman zum Zeitpunkt des Kinostarts bereits gelesen hatten, gaben 60% an, die Verfilmung gesehen zu haben.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass eine aus den Befragten zufällig ausgewählte Person, die laut Umfrage den Roman zum Zeitpunkt des Kinostarts noch nicht gelesen hatte, angab, die Verfilmung gesehen zu haben."
Gemeint ist wohl, dass die Umfrageergebnisse als Wahrscheinlichkeiten gedeutet werden.
>0.18-0.12*0.60
0.108
Etwas tricky und womöglich mit bedingten Erwartungen gedacht, vielleicht auch schulgemäß als Ereignisbaum. 0.12=1-0.88 der Befragen haben das Buch gelesen, also hat der Anteil
![]()
das Buch gelesen und den Film gesehen. Damit lässt sich berechnen, wie viele das Buch nicht gelesen, aber den Film gesehen haben. Geteilt durch die Gesamtzahl der Nichtleser erhalten wir die gesuchte Wahrscheinlichkeit.
>0.108/0.88
0.122727272727
"Betrachtet werden folgende Ereignisse:
R: Eine aus den Befragten zufällig ausgewählte Person hatte laut Umfrage den Roman zum Zeitpunkt des Kinostarts bereits gelesen.
V: Eine aus den Befragten zufällig ausgewählte Person sah laut Umfrage die Verfilmung.
Beschreiben Sie das Ereignis
![]()
im Sachzusammenhang und bestimmen Sie die Wahrscheinlichkeit dieses Ereignisses."
>0.12*0.4+0.88
0.928
Diese Aufgabe ist wieder seltsam gestellt. R und V sind keine Mengen eines Zufallsraums sondern eher Zufallsvariablen. Aber gemeint ist natürlich die Wahrscheinlichkeit, dass jemand den Film nicht gesehen oder das Buch nicht gelesen hat. Man beachte, dass die Ereignisse R und V nicht unabhängig sind!
"Ein Jahr später möchte die Tageszeitung ermitteln, ob sich durch die Verfilmung der Anteil p der Jugendlichen, die den Roman gelesen haben, wesentlich erhöht hat. Die Nullhypothese
![]()
soll mithilfe einer Stichprobe von 100 Jugendlichen auf einem Signifikanzniveau von 10% getestet werden. Bestimmen Sie die zugehörige Entscheidungsregel."
>invbindis(0.95,100,0.15), bindis([20,21],100,0.15)
20.6035042646 [0.93368, 0.960722]
Das bedeutet: Wenn unter der Annahme p=0.15 von 0 bis 20 Personen gefunden werden, die das Buch gelesen haben, so kann man die Annahme nicht ablehnen. Erst bei 21 Personen ist dies mit einem Fehler von 4% möglich.
Das folgende Beispiel ist von der Seite
D. Koller - Einführung des Begriffs der Ableitung
>function d(t) &= 1/(1+exp(-0.05*(t-60)))
1
--------------------
- 0.05 (t - 60)
E + 1
Diese Formel gebe das Wachstum des Stammdurchmessers einer Fichte an. Wie immer ist es sinnvoll über diese Formel zu dislutieren. Wo könnte sie her kommen? Wie kann man sie verifizieren? Macht sie überhaupt Sinn? Was bedeuten die Parameter? Sicher gibt es noch viele andere gute Fragen.
Die erste Aufgabe auf der verlinkten Seite lautet lapidar: Verschaffe dir einen Überblick über das "Wachstum" des Stammdurchmessers der Fichte in den ersten 200 Jahren.
>plot2d("d",0,200):
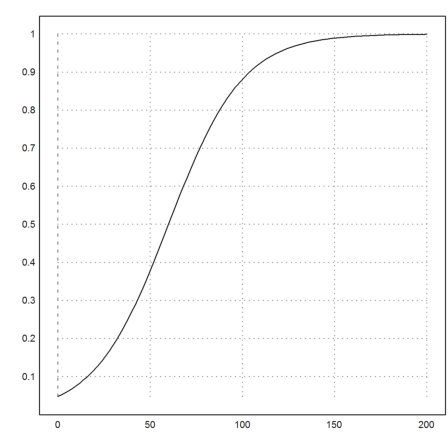
Man erkennt den Grenzwert 1, der auch schon aus der Formel bekannt ist.
Nun werden Differenzenquotienten untersucht. Der Autor will damit verhindern, dass der Begriff der Ableitung lediglich über die Tangente aufgenommen wird. Die Definition der mittlenen Änderungsrate zwischen x und x+dx lautet formal
![]()
Es wird also die Wachstumsgeschwindigkeit als Wachstum/Zeitraum motiviert.
>(d(10.1)-d(10))/0.1
0.00351262777096
In Euler ist es sinnvoll, diesen Quotienten in einer Funktion abzulegen.
>function md(x,dx) := (d(x+dx)-d(x))/dx; >md(10,0.1)
0.00351262777096
Man kann diese Funktion auch gleich auf einen Vektor von dx anwenden. Diesen Schritt versteht man nur, wenn man Vorkenntnisse in der Matrixsprache von Euler hat.
>md(10,[1,0.1,0.01,0.001]')
0.00358037 0.00351263 0.00350593 0.00350526
Der Quotient strebt gegen eine Grenzwert. Das ist anschaulich klar, wenn man die Funktion sieht. Sie ist zwischen 10 und 11 praktisch eine Gerade.
>plot2d("d",10,11):
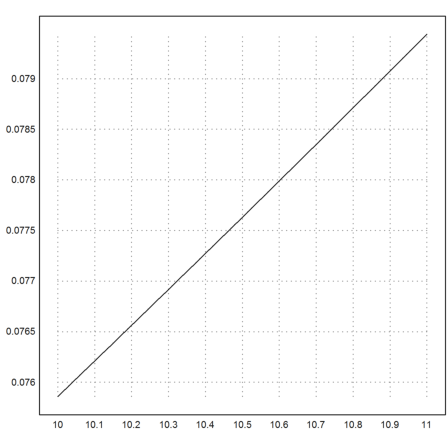
Die Ableitung wird auf der verlinkten Seite als Grenzwert vorgestellt. Dann wird eine Funktion geschrieben, die solche Grenzwerte für gegebenes d(x) ausrechnet. In Euler ist das eine rein symbolische Funktion.
>function wd(x) &&= limit((d(x+dx)-d(x))/dx,dx,0)
d(x + dx) - d(x)
limit(----------------, dx, 0)
dx
Wir testen das an folgendem Beispiel.
>function d(x) &= x^3-10*x
3
x - 10 x
Maxima rechnet die Grenzwerte, genau wie Maple, aus. Sowohl in einzelnen Punkten, als auch allgemein.
>&wd(5)
65
>&wd(x)
2
3 x - 10
Es ist dann möglich, die Funktion und die Ableitung in denselben Graph zu plotten.
>plot2d(&d(x),-4,4); plot2d(&wd(x),>add,color=red):
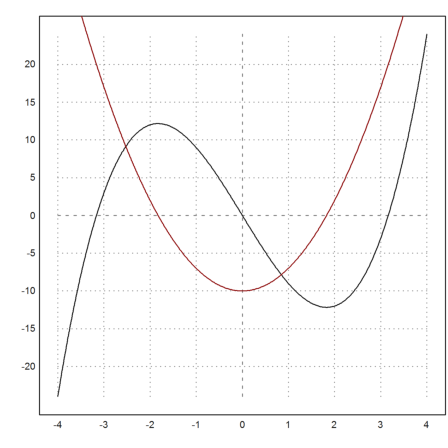
Definieren wir unsere Originalfunktion nochmals.
>function d(t) &= 1/(1+exp(-0.05*(t-60)));
Dann können wir die Ableitung plotten. Aus Gründen, die dem Schüler nicht verständlich sein dürften, fragt Maxima hier nach, ob x/10 ganzzahlig ist. Euler beantwortet das automatisch mit "unknown".
>plot2d(&wd(x),0,200):
Answering "Is x/10 an ?integer?" with "unknown" Answering "Is x/10 an ?integer?" with "unknown"
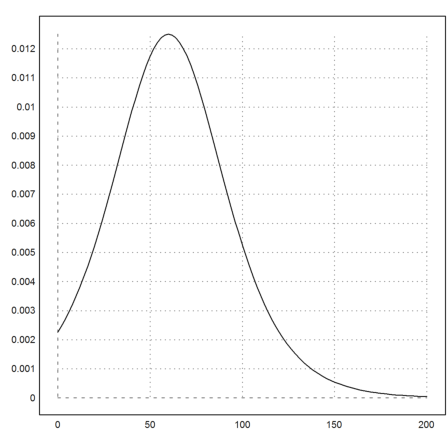
Der Grund liegt darin, dass Maxima hier eine Methode anwendet um den folgenden Grenzwert zu berechnen, die nicht ganz offensichtlich ist.
>&factor((d(x+dx)-d(x))/dx)
dx/20 x/20 + 3
(E - 1) E
------------------------------------
x/20 + dx/20 3 x/20 3
dx (E + E ) (E + E )
Man kann sich darüber streiten, ob es sinnvoll ist, dem CAS eine für den Schüler nicht durchschaubare Berechnung eines Grenzwertes zu überlassen. Die Idee des "Calculus" ist ja gerade, solche schwierige Grenzwerte nicht berechnen zu müssen.
Wenn man das macht, so liegt es näher, bei numerischen Lösungen zu bleiben. Das geht etwa so.
>plot2d("md(x,0.1)",0,200):
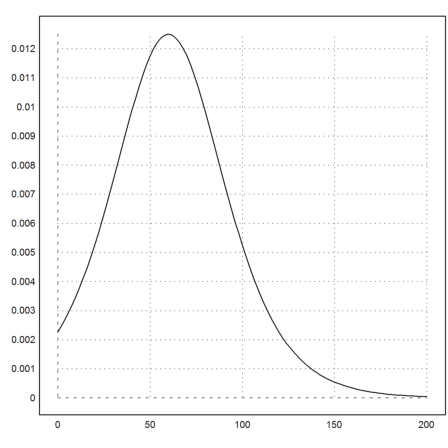
Für den Schüler ist das befriedigend. Man hat danach Mühe, ihn von der Notwendigkeit des Erlernens algebraischer Ableitungen zu überzeugen. Es sollte aber dafür genügend Argumente geben, oder?
Interessant ist auch die folgende Idee des Papers, die die Sekantengleichung herleitet.
>forget f; seceq &= (y-f(x0))/(x-x0)=(f(x1)-f(x0))/(x1-x0)
y - f(x0) f(x1) - f(x0)
--------- = -------------
x - x0 x1 - x0
>function f(x) &= x^3-x; >function sect(x,x0,y0,x1,y1) &= y with solve(seceq,y)
3 3 3
- (x0 - x) (x1 - x1) + (x0 - x0) x1 - x (x0 - x0)
----------------------------------------------------
x1 - x0
Auf der verlinkten Seite wird nun noch eine Folge von Sekanten geplottet. Wir machen das mit Hilfe der Matrixsprache von Euler nach, obwohl es mit Hilfe von Maxima möglich wäre die symbolische Herangehensweise von Maple nachzuahmen.
Zunächst plotten wir die Funktion. Wenn Sie den Plot nicht sehen, drücken Sie die Tabulator-Taste.
>plot2d("f(x)",-1,4,-20,20,color=red,thickness=3);
Nun werden x0, y0 und eine Folge von Punkte x1, y1 auf der Kurve erzeugt.
>x0=1.5; y0=f(x0); x1=1.5+0.8^(-3:22); y1=f(x1);
Nun werten wir alle Sekanten for x=-4 bis x=4 aus, und fügen alle gleichzeitig dazu.
Es wäre hier wahrscheinlich einfacher, eine Schleife zu verwenden. Dann braucht man nichts von der Matrixsprache von Euler zu verstehen.
>x=-4:4; plot2d(x,sect(x,x0',y0',x1',y1'),>add,color=green);
Schließlich fügen wir noch die Punkte dazu.
>plot2d(x1,y1,>points,color=blue,>add):
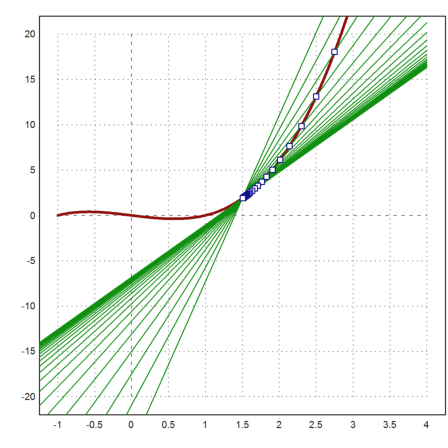
Das folgende Beispiel stammt aus
"Ein Tank enthält anfänglich 1000l reines Wasser. Mit einer Rate von 10l pro Minute fließt eine Salzlösung zu, bei der pro Liter 200g Salz gelöst sind. Gleichzeitig fließen pro Minute 10l der Salzmischung wieder aus."
Dies ist ein interessantes Problem, über das man zunächst ohne Fragestellung diskutieren sollte. Die Schüler sollten selbst die Fragen stellen. Vielleicht gelangen sie zu anderen Vorgehensweisen, als der folgenden.
Wenn q(t) der Salzgehalt im Fass ist, so fließen 2g/min zu und 1% des Salzes pro Minute ab. Wir erhalten die Differentialgleichung
>eq &= 'diff(q,t)=2-(10/1000)*q
dq q
-- = 2 - ---
dt 100
Das kann man mit Maxima automatisch lösen. Man kann dann eine Funktion mit einer Konstanten definieren. Es ist auch leicht zu sehen, dass die Konstante -200 sein muss, wenn q(0)=0 ist.
>&ode2(eq,q,t), &expand(q with %), function q(t) &= % with [%c=-200]
- t/100 t/100
q = E (200 E + %c)
- t/100
%c E + 200
- t/100
200 - 200 E
In Euler gibt es Funktionen für Vektorfelder.
>vectorfield("2-0.01*y",0,500,0,200); ...
plot2d(q,color=red,thickness=2,>add,yl="kg",xl="min"):
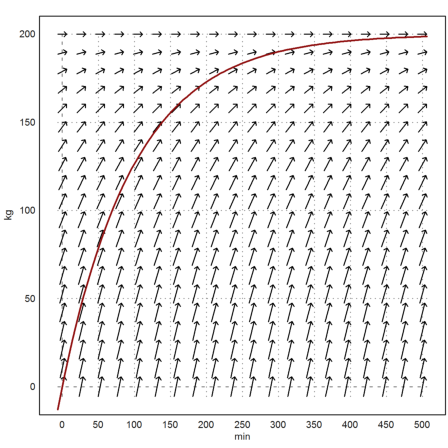
Wie lange dauert es, bis der Salzgehalt 10kg beträgt.
>solve(q,0,y=10)
5.12932943876
Eine Alternative, über die man trefflich diskutieren kann, wäre es, die Wasserhähne nacheinander für eine Minute zu öffnen. Das führt auf eine rekursive Folge.
>v=iterate("x+2-0.01*x",0,500);
Hier sind die ersten Glieder.
>v[1:20]
[0, 2, 3.98, 5.9402, 7.8808, 9.80199, 11.704, 13.5869, 15.4511, 17.2966, 19.1236, 20.9323, 22.723, 24.4958, 26.2508, 27.9883, 29.7084, 31.4114, 33.0972, 34.7663]
Offenbar unterscheidet sich das nicht wesentlich von der Lösung der Differentialgleichung.
>plot2d(0|v); plot2d(q,color=red,>add):
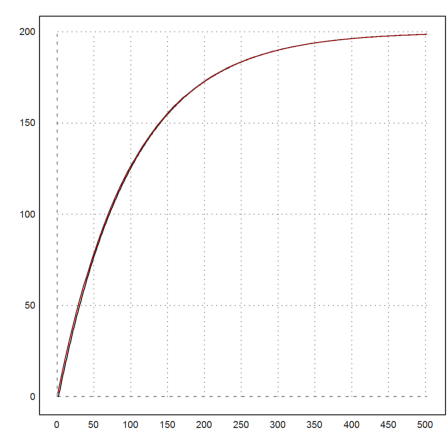
Es ist interessant, die Gleichung zu finden, wenn
![]()
gegeben ist. Dann hat man
![]()
In unserem Fall erhält man tatsächlich das Folgende.
>v[50], 200*(1-0.99^50)
77.7765520934 78.9987865725
Es ist interessant sich zu überlegen, dass die kontinuierliche Lösung also die folgende Näherung bedeutet.
![]()
Dies wirkt sich auf die Werte von q(n) und v[n] aus.
>200-200*E^(-50/100), 200-200*(1-1/100)^50
78.6938680575 78.9987865725
Geometrische Vermessungsaufgaben sind eine großartige Methode, Theorie und Praxis der Mathematik zu vereinbaren. Schon Gauß wurde durch diese praktische Tätigkeit zu Erkenntnissen angeregt. Vermutlich war er eher ein zerstreuter Geometer.
Für die folgenden Rechnungen nehmen wir exakte Punkte an und simulieren eine Messung durch Rundung der exakten Ergebnisse. Wir rechnen damit einmal normal, und einmal mit Intervallkontrolle.
Die Aufgabe besteht darin, die Entfernung und Höhe von C zu berechnen. Die Punkte A, B, C seien exakt die Folgenden.
>A=[12,13,0]; B=[125,29,12]; C=[81,2984,511];
Wir bestimmen die Messwerte aus gerundeten exakten Werten. In der Praxis wäre eine tatsächliche Messung eine echte Herausforderung.
Der Abstand von AB werde folgendermaßen gemessen.
>AB=round(norm(A-B),2)
114.76
Die Winkel CAB und CBA werden ebenfalls gemessen. Wir runden auf 1/100 Grad.
Zunächst eine Funktion für Winkel.
>function angle(A,B,C) := acos(scalp(A-B,C-B)/(norm(A-B)*norm(C-B))); >CAB=round(deg(angle(C,A,B)),2), CBA=round(deg(angle(C,B,A)),2)
79.77 98.07
Der Winkel bei C kann dann berechnet werden.
>ACB=180-CAB-CBA
2.16
Aus dem Sinussatz folgen die beiden Abstände AC und BC.
>AC=AB/sin(ACB°)*sin(CBA°), BC=AB/sin(ACB°)*sin(CAB°)
3014.67273005 2996.42038817
Korrekt sind die folgenden Werte.
>norm(A-C), norm(C-B)
3015.41423357 2997.15898811
In Euler kann man diese Rechung mit Intervallen durchführen. Dadurch wird das Ergebnis garantiert eingeschlossen.
Zunächst definieren wir die Intervalle, wobei eine maximale Abweichung von 1/200 annehmen. Dies entspricht unserer Rundung auf 1/100 Grad.
>iCAB=CAB±0.005; iCBA=CBA±0.005; iAB=AB±0.005;
Die Intervalle werden etwas übergroß ausgegeben. Sie sind aber korrekt.
>iAB, left(iAB), right(iAB)
~114.75,114.77~ 114.755 114.765
Nun führen wir die Rechnung mit Intervallen durch.
>iACB=180-iCAB-iCBA
~2.15,2.17~
>iCA=iAB/sin(iACB°)*sin(iCBA°), iCB=iAB/sin(iACB°)*sin(iCAB°)
~3000,3029~ ~2982,3011~
Um die Höhe des Berges zu berechnen, sei noch die Erhebung von B über dem Niveau von A und von C über dem Niveau von B bekannt.
>gB=[B[1],B[2],A[3]]; wB=round(deg(angle(gB,A,B)),2)
6
>gC=[C[1],C[2],B[3]]; wC=round(deg(angle(gC,B,C)),2)
9.58
Aus diesen "Messwerten" lässt sich nun die Höhe des Berges über dem Niveau von A berechnen.
>AB*sin(wB°)+BC*sin(wC°)
510.673628178
Das korrekte Ergebnis ist davon etwas entfernt.
>C[3]-A[3]
511
Führen wir zur Kontrolle eine Messung von A direkt aus.
>gAC=[C[1],C[2],A[3]]; wAC=round(deg(angle(gAC,A,C)),2)
9.76
>AC*sin(wAC°)
511.051883155
Auch diese beiden Rechnungen kann man intervallmäig durchführen.
>iwB=wB±0.005; iwC=wC±0.005; iwAC=wAC±0.005;
Wir können die Intervalle der beiden Messungen miteinander schneiden. Allerdings ist das Ergebnis noch immer recht grob.
>(iAB*sin(iwB°)+iCB*sin(iwC°))&&(iCA*sin(iwAC°))
~508.4,513.3~